Option Model Handbook, Part II: Introduction to Binomial Trees

Introduction to Binomial Trees

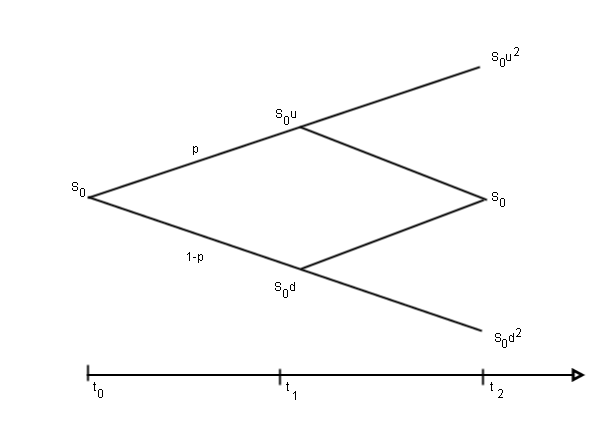
Let us construct a tree whose pricing is given as shown in the figure above, restricting to time $t_0$ and $t_1$. Initial price of the stock is $S_0$ at $t_0$ and has the possibility of moving to $S_0u$ or $S_0d$ at time $t_1$. Let $p$ be the probability of the price to rise from $S_0$ to $S_0u$. Calculating the expected return from the stock at $t_1$ and making use of risk-neutral valuation

$$ E(S_{t_1}) = pS_0u + (1-p)S_0d = S_0 e^{r(t_1-t_0)} $$

we get,

\begin{equation} \label{eq:btp} p = \frac{e^{r(t_1-t_0)} - d}{u - d} \end{equation}

We need to chose appropriate values for the parameters $u$ and $d$ which can be obtained from equating the variance of the return to $\sigma^2 \Delta t$. The variance of the stock price return on the binomial tree is:

$$ pu^2 + (1−p)d^2 − [ pu+ (1−p)d]^2 = \sigma^2 \Delta t $$

On ignoring terms of order higher than $\Delta t^2$ and making use of $ud = 1$, we get

\begin{equation} u = e^{\sigma \sqrt{\Delta t}} \nonumber \end{equation} \begin{equation} d = e^{-\sigma\sqrt{\Delta t}} \end{equation}

One can make use of the above construction to value an option. Let $f$ be the current value of an option on a stock. Let the payoff of the option after one step (time T) on a binomial tree be $f_u$ and $f_d$ for up and down movement of the stock respectively. The value of the option in this case is given as:

$$ f = e^{−rT}[ pf_u + (1−p)f_d] $$.